2024年4月に開設した大学院に通う、修士1年生の牧将太さんに現在の研究活動についてインタビューを行いました。インタビューは2024年10月時点のものです。

牧さんは本学情報学部で4年間を過ごした後、大学院である地域情報学研究科に進学し、渡邉扇之介准教授のゼミで活動しています。

研究テーマ

Max-plus代数における矩形（くけい）行列の行列式

研究概要

大学数学における線形代数で学ぶ行列の行列式の概念は、行列の行数と列数が等しい行列に対して定義されます。Max-plus代数とは使うことのできる演算を「Max（最大値）」と「Plus（足し算）」に限定した数学で、この代数における行列の行列式を計算すると行列から決まる２部グラフの最適マッチングが得られることが知られています。「2部グラフの最適マッチング」とは、例えば「社員」と「仕事」という2つの属性に対して、最も適切なペアを求める最適化問題です。私は、Max-plus代数上で行数と列数が異なる行列に対して行列式を定義したときにどのような最適化問題で説明でき、行列式の値からその最適化問題に対して何が得られるかに興味があり研究を行っています。

学部時代での研究課題

高校では理系で数学が割と得意だったことや、兄が福知山公立大学に在籍していたので評判や情報学部が新設されることを知って入学を決意しました。渡邉ゼミに所属して間もなく、3つの研究テーマ「最適化」「Max-plus代数」「セルオートマトン」のうち、自分の好きなものを選ぶ機会があり、唯一単語から連想しやすい「最適化」を選択し、2年生までプログラミングにも挑戦しながら研究していました。

卒業論文を意識し始めた3年生で、最適化で導き出していた結果が、Max-plus代数を使っても表現できることを渡邉先生から助言いただき、「おもしろそう」と感じたことをきっかけにMax-plus代数を用いた研究に没頭し、「Max-plus代数を用いたヒープモデルの考察」というテーマで卒業論文を書きました。ヒープモデルは、箱の中にテトリスのような図形を詰め込むことを考えた数学モデルで、生産工程や日程などのスケニューリング、荷物や在庫の保管・輸送の最適化などに応用される。このモデルをMax-plus代数を用いて数式で表し、最適解を求めるということを考えました。

大学院では、どんな研究に取り組んでいますか

学部での研究が楽しく、このまま続けたいと思っていた矢先に大学院の新設が決まり、進学しました。正方形での行列式で研究していた学部時代でしたが、その基礎知識をもって矩形行列（いわば、長方形）での行列式を研究しています。研究はPCに向かうのではなく、基本的にはノートに数式や図をひたすら書き込んでいる時間の方が長いです。

2024年8月には台風の影響により現地参加は断念しましたが、第22回計算数学研究会でのポスター発表や、翌月の第2回福知山数理・データサイエンス研究会でもポスター発表を行い、質疑応答で出席者からの鋭い意見をいただき、これからの研究に反映していきたいと考えています。

先生からはどんな指導がありますか

渡邉ゼミでは毎週金曜日の午後に時間が設けられており、それぞれ研究に取り組んだり、行き詰ったところを先生に相談したりしています。学部時代から渡邉先生には研究の転機となるアドバイスをいただくことがあり、いつも気づきを与えてくださいます。

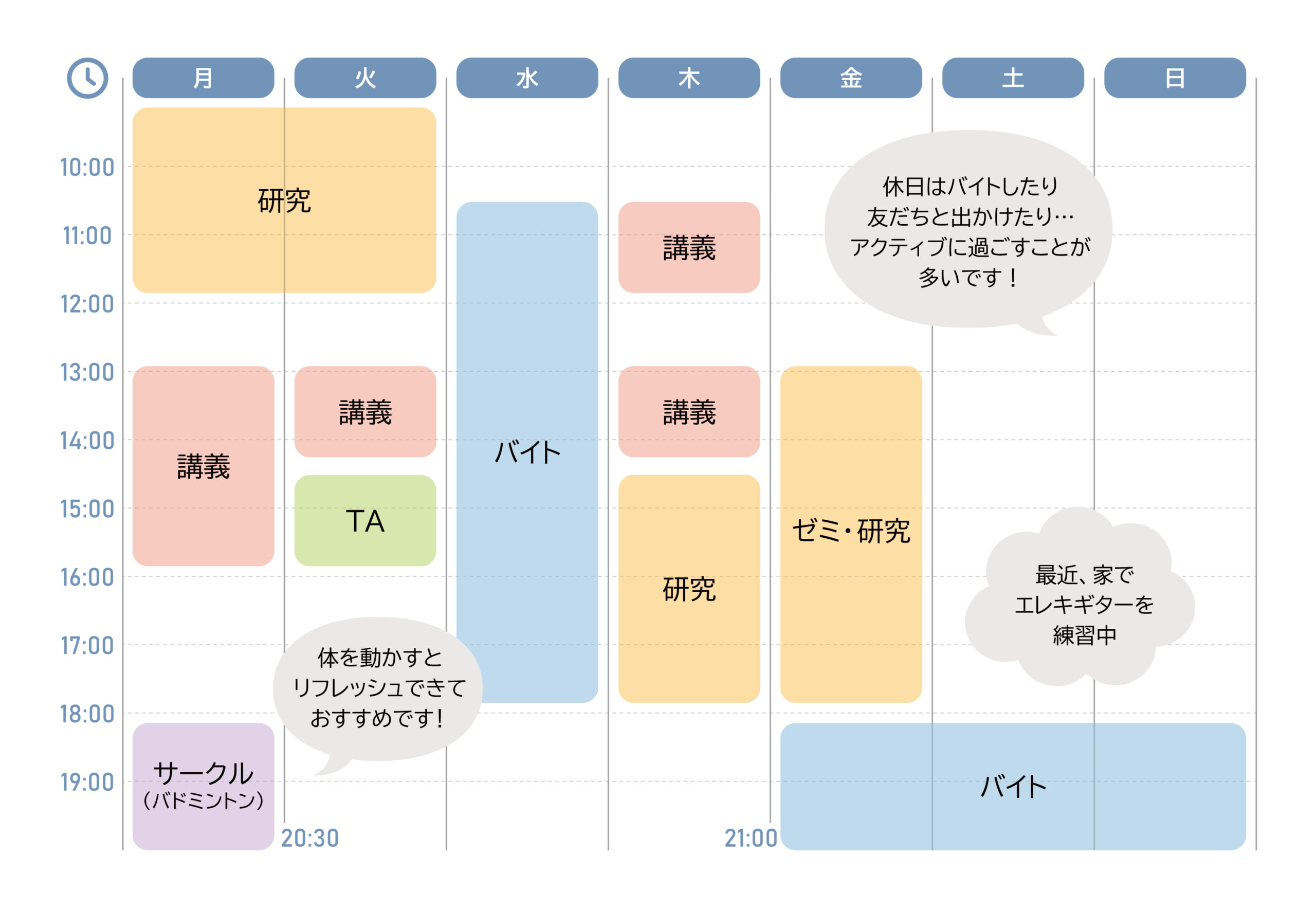
1週間のスケジュール

「2年生で研究に専念できる自由な時間を生み出すために、1年生でなるべく単位を取得しておくといい」と渡邉先生からのアドバイスもあり、修士1年生の後期では、月・火・木に計5科目の講義を履修しています。休みと研究は割と区別していますが、講義前後に研究したりと、大学にいる時は基本的に研究しています。自分の場合は、ファッションが好きで洋服代や生活費の捻出のため2つのバイトを掛け持ちしています。あと、火曜4限には情報学部の演習科目「数学演習Ⅱ」のTA（ティーチング・アシスタント）として学部生が授業中に分からない部分の補助や指導を行っています。

研究やバイトの息抜きとしては、毎週月曜にあるバトミントンサークルで運動不足を解消すること。研究は黙々と作業しているのに対して、サークルではみんなと楽しくおもいっきり体を動かしています。

大学院をめざす方へメッセージ

大学院修士課程で得た知識は、就職活動の際にも幅の広がりを感じ、有利だと感じています。研究が好きで進学しましたが、学会や研究会への参加で発表しながらスキルを磨き、思い出づくりにもなっています。ぜひ研究が好きなら大学院への道を進んでみてください。